Esta publicación trata sobre el teorema del seno, uno de los teoremas más importantes de la trigonometría. Este teorema permite su aplicación para calcular la longitud de los lados de cualquier triángulo o la medida de sus ángulos. Por lo tanto, en la publicación de hoy, explicaremos con detalle qué es el teorema del seno y cómo se aplica a ejemplos específicos y problemas matemáticos. La página incluye un videotutorial al final que muestra claramente cómo se define el teorema del seno para diferentes triángulos.
¿Cómo se define el teorema del seno?
Para obtener el teorema que llamamos teorema del seno, un triángulo debe dividirse en dos triángulos rectángulos disminuyendo una de sus tres alturas. La longitud de la altura es el lado común de ambos triángulos rectángulos. Su longitud se expresa en función del primer y segundo triángulo, por lo que, dado que ambas expresiones tienen resultados idénticos, podemos igualarlas. Así es como se define. Observa la imagen de abajo y observa cómo un triángulo se divide en dos triángulos rectángulos disminuyendo una de sus alturas.
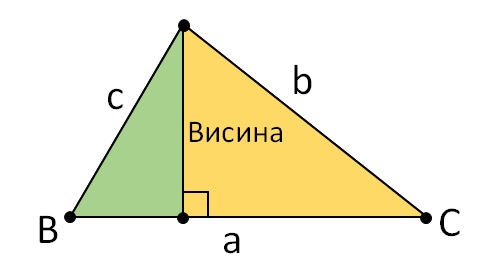
Para el triángulo verde de la imagen de arriba, podemos escribir las siguientes fórmulas:
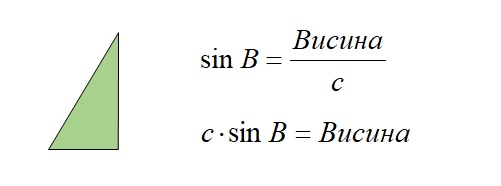
De la misma manera, se pueden derivar las siguientes fórmulas para el triángulo naranja:

Lógicamente, dado que ambas fórmulas (de los triángulos verde y naranja) son iguales a la longitud de la altura, podemos escribir que son iguales. La fórmula se aplica:
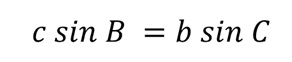
¿De dónde podemos derivar la conclusión para la primera parte del teorema del seno:

Si repetimos este proceso bajando las tres alturas de la misma manera, obtendremos el contenido completo del teorema del seno, que dice:
Aplicación del teorema del seno
¡Su aplicación es enorme! Este teorema es uno de los más utilizados en trigonometría, geometría y matemáticas en general. Su principal aplicación es determinar la longitud de un lado desconocido o la medida de un ángulo en un triángulo cuya medida desconocemos.
A continuación, puedes ver un ejemplo de cálculo de la longitud de un lado y la medida de un ángulo de un triángulo utilizando el teorema de los senos.
Ejemplo 1: Calcula la longitud del lado x del triángulo de la imagen de abajo.

A partir de los datos de la imagen superior, se comprende fácilmente que disponemos de datos suficientes para aplicar el teorema del seno. La relación que debemos establecer es:
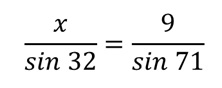
De lo cual se sigue que:

Calculando los valores de las funciones trigonométricas se obtiene el resultado final, que se relaciona con la longitud del lado desconocido del triángulo:

Ejemplo 2. ¡Calcula el tamaño del ángulo x en el triángulo de la figura a continuación!
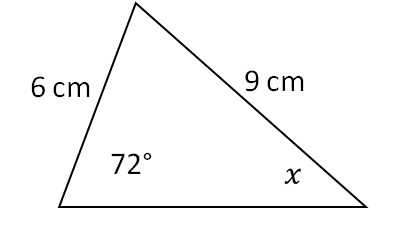
Aplicando el teorema del seno, escribimos la relación:
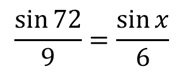
De lo cual se sigue que:
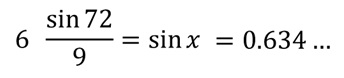
Para determinar finalmente de forma fácil el tamaño del ángulo desconocido:
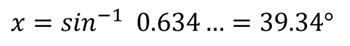
Pruebas en video y ejemplos
El video, disponible con un solo clic a continuación, contiene una demostración de cómo se define el teorema para varios triángulos. También puedes ver en el video una gran cantidad de ejemplos resueltos donde se determinan las longitudes de los lados de diferentes triángulos o la magnitud de sus ángulos mediante el teorema de senos. ¡Te recomendamos revisar tantos ejemplos como puedas!
Tags: Ejemplo, Fórmula, Seno, Teorema, Teorema Del Seno


 Espere por favor...
Espere por favor...